A csillagászat elemei I. A Kepler-törvények és néhány alkalmazásuk (1) – Csizmadia Szilárd
Johannes Kepler német csillagász 1609-ben tette közzé a bolygómozgásokra vonatkozó első két, és 1619-ben a harmadik törvényét.
Ebben a fejezetben Kepler I. törvényével fogunk foglalkozni.
Ez a törvénye így hangzik:
A bolygók olyan ellipszis alakú pályán mozognak a Nap körül, amelyek egyik gyújtópontjában a Nap áll.
Ma már tudjuk, hogy a törvény ennél sokkal általánosabb: más bolygórendszerekre, sőt kettőscsillagokra is vonatkozik. Amennyiben két galaxis vagy két nyílthalmaz igen távol van egymástól (tehát az árapályerőktől és a nem pontszerű tömegeloszlástól eltekinthetünk), még az egymás körül keringő galaxisokra vagy nyílthalmazokra is alkalmazható.
A törvény alkalmazásához érdemes felidézni az ellipszis néhány tulajdonságát.

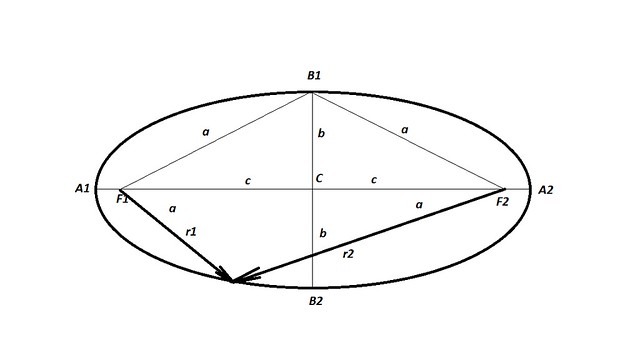
Az ellipszisnek két gyújtópontja van, amelyeket az 1. ábrán F1-gyel és F2-vel jelölünk. Az ellipszis azon pontok halmaza egy síkon, amelyeknek az F1-től és az F2-től mért távolságának összege állandó:
(1)
Amennyiben az F1 és F2 gyújtópontok – nevezik őket fókuszpontoknak is – egybeesnek, akkor kört kapunk. A kör tehát az ellipszis speciális esete.
Ebből következik, hogy ha egy falapra leszúrunk két szöget és azokhoz rögzítünk egy-egy madzagot, akkor ellipszist rajzolhatunk a madzagok összekötött közös végeire tett ceruzával. A kör rajzolását 1:30-tól, az ellipszisét 5:05-től mutatja be ez a videó, ami asztalosmunkákat ismertet.
Az egyik gyújtóponttól az ellipszis egy pontjáig húzott egyenest vezérsugárnak nevezzük. A bolygót és a Napot összekötő egyenes tehát a vezérsugár. Az 1. ábrán, ha a Nap pl. az F1 fókuszpontban van, akkor az r1 szakasz lehet a vezérsugár.
Az ellipszis nagytengelye az ellipszis két átellenes pontját úgy köti össze, hogy a két fókuszpont ráesik. A csillagászati gyakorlatban ennek felét, a fél nagytengelyt szoktuk használni, és a-val jelöljük. A két fókuszpont között van félúton az ellipszis C-vel jelölt centruma.
Az ellipszis kistengelye a C középpontban a nagytengelyre állított azon merőleges szakasz hossza, aminek végpontjait a szakasszal egybeeső egyenesnek az ellipszissel való metszéspontjai jelölnek ki. A kistengely hossza helyett is a fél kistengelyhoszt használjuk, amit b-vel jelölünk.
A centrum és az egyik fókuszpont távolsága a lineáris excentricitás, amit c-vel jelölünk. Be lehet bizonyítani – de ezt a bizonyítást a középiskolai matematika órákra meghagyjuk -, hogy
(2)
Vagyis a fél nagytengely négyzete egyenlő a kistengely és a lineáris excentricitás négyzeteinek összegével. A fél nagytengelyek végei, a B1 és a B2 pontok tehát a fókuszpontoktól éppen fél nagytengelynyi távolságra vannak. A bolygók tehát éppen akkor vannak fél nagytengelynyi távolságra a Naptól, amikor a kistengely végpontjaira érnek pályájukon.
A pálya elnyúltságát az excentricitással mérjük. A csillagászatban a lineáris excentricitás helyett inkább a numerikus excentricitást használjuk, amit e-vel jelölük és ami egyszerűen a lineáris excentricitásnak a pálya fél nagytengelyéhez viszonyított hossza:
(3)
A (3)-ik egyenletet a másodikba téve és némi egyenletrendezést végrehajtva, egy, a csillagászatban nagyon gyakran használt összefüggést kapunk:
(4)
A (4)-ik egyenlet szerint függ tehát az excentricitás az ellipszispálya b kistengelyétől és a nagytengelyétől. Mint említettük, e a numerikus excentricitás lenne, de a csillagászatban és másutt sokszor elhagyják a numerikus jelzőt, és csak excentricitásnak nevezik. Jobb helyeken azonban megadják ezek neveit. Nagyon régen használták az ún. excentricitási szöget: , ami lényegében annak a szögnek a szinusza, amennyivel egy kört meg kell dönteni ahhoz, hogy vetületben az adott excentricitású ellipszist lássuk. A mai csillagászati gyakorlatban ez a szög már szinte soha nem fordul elő (vizuális valódi kettőscsillagok modellezésében nagy néha használják még).
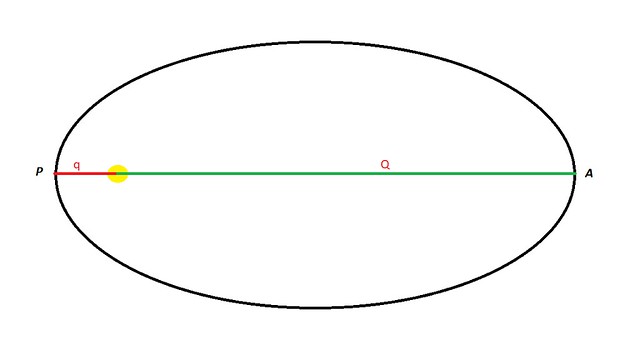
A 2. ábrán az ellipszispályán mozgó égitestnek a pályáján a legkisebb közelségét (P) és legnagyobb távolságát (A) jelöltük be. Napközelpontnak a Nap és a bolygó legkisebb távolságát (jele: q), naptávolpontnak a Nap és a bolygó legnagyobb távolságát nevezik (jele: Q). Ezek természetesen a nagytengelyre esnek, és a 2. ábrán P és A jelöli őket. P a perihélium (napközel), A az afélium (naptávol) görög eredetű szó rövidítése. Ellipszispálya sok más esetben is megvalósul. Pl. a Hold vagy egy műhold a Föld körül földközelben (perigeum) vagy földtávolban (apogeum) van. A Jupiter holdjai esetében jupiterközelről (perijovium) vagy jupitertávolról (apojovium) beszélünk. Egy kettőscsillag esetén a két csillag közelpontját periasztronnak, legnagyobb távolságának pontját apasztronnak nevezzük (előfordul aposztron is néha-néha…). Ugyanígy, egy exobolygó a csillaga körül periasztronban vagy apasztronban lehet. Könnyű rájönni, hogy a peri mindig a közelpont, az apo a távolpont összetételében fordul elő. Megjegyzendő, hogy így használva a görög eredetű szó latinizált magyaros változatát emlegetjük. (Angolul a megfelelő szakszavak: perihelion, aphelion, perigee, apogee. perijovian, apojovian, periastron, apastron).
A csillagászatban két szöget: az excentrikus anomáliát (jele: E) és a valódi anomáliát (nemzetközileg inkább f-fel jelölik, a magyar tankönyvekben inkább v-vel, eredetileg pedig görög nü lehetett) különösen sokat használnak. A 3. ábra mutatja e két szög jelentését:
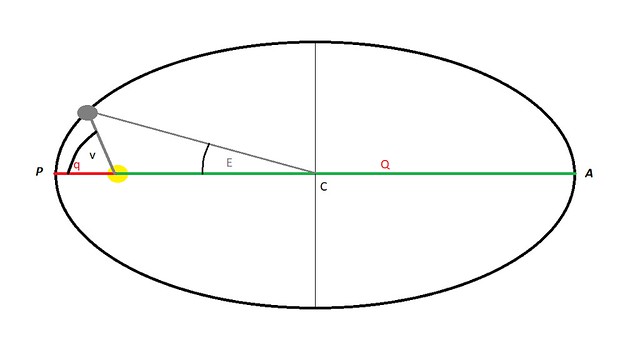
Excentrikus anomália: az ellipszis C centrumánál lévő szög, amely a csillag (vagy ezzel egyenértékűen a P közelpont) és a bolygó által bezárt szöget adja meg.
Valódi anomália: a csillag (bolygó stb. vonzótest) által elfoglalt gyújtópontban lévő szög, amely a csillagtól stb. nézve a közelpont iránya és a bolygó (hold stb.) felé húzott egyenes közti szöget adja meg.
Mindezek ismeretében végre megadhatjuk Kepler I. törvényének matematikai alakját.
Az excentrikus anomáliával kifejezve az I. törvény az alábbi alakban írható:
(5) ,
a valódi anomáliával kifejezve pedig
(6)
Néha az egyik, néha a másik kifejezés használata az egyszerűbb vagy a célszerűbb.
- feladat:
Kepler I. törvénye alapján határozzuk meg, hogy hogyan lehet kifejezni egy bolygó napközelségét és naptávolságát a fél nagytengely és az excentricitás segítségével!
Megoldás:
Napközelben a Nap-bolygó távolság q, a naptávolság Q:
Itt E1 és E2 az excentrikus anomália értéke napközelben, illetve naptávolban. A 3. ábrára tekintve nyilvánvaló, hogy E1 = 0° napközelben és E2 = 180° naptávolban. 0° koszinusza 1, 180° koszinusza pedig -1. Ezeket behelyettesítve kapjuk, hogy
(7)
A napközelség és a naptávolság tehát a fél nagytengely és az excentricitás függvénye. Hasonlóképpen, egy kettőscsillagban a két csillag legkisebb és legnagyobb távolságát is fél nagytengelyük és excentricitásuk határozza meg.
Ha pl. körpályán mozog a bolygó a Nap körül, akkor az excentricitás nulla (e=0), a pálya kistengelye és nagytengelye egyforma. Ekor q=Q, vagyis a pálya minden egyes pontja napközelpont és naptávolpont egyszerre. (Nyilván ilyenkor nincs értelme napközelről és naptávolról beszélni, körpályán a két égitest egymástól mért távolsága nem változik.)
Eredményünk a Nap körül mozgó üstökösökre és kisbolygókra is igaz (sőt, minden Nap körül a kölcsönös gravitációs erő hatására, vagy két, egymás körül a kölcsönös gravitációs vonzás hatására keringő égitestre igaz). Az üstökösök pályája gyakran nagyon elnyúlt, az excentricitás 0,9 is lehet. A (4)-ik egyenletből kiszámolható, hogy ilyenkor a kistengely és a nagytengely méretaránya
,
vagyis a kistengely a nagytengely hosszának 43,6%-a. Az is kiszámolható, hogy egy ilyen égitestnek a napközelpontja a fél nagytengely 10%-ára van a Naptól, naptávolpontja meg 190%-ára:
.
Ha pl. az üstököspálya fél nagytengelye 20 Csillagászati Egység (CSE), akkor a napközelpont 2 CSE-re van a Naptól, a naptávolpont pedig 38 CSE-re az adott e=0,9-es excentricitás esetére.
2. feladat
Az előző feladat fordítottja: ha tudjuk, hogy egy üstökös naptávolban 21,5 CSE-re jár a Naptól, napközelben pedig 0,5 CSE-re, akkor mennyi az üstököspálya fél nagytengelye és excentricitása?
A megoldáshoz írjuk egymás alá a napközelséget és a naptávolságot kifejező egyenletet:
A két egyenletet összeadva kapjuk, hogy:
,
amiből a fél nagytengely:
A megadott számérékeket behelyettesítve a fél nagytengelyre a=11 CSE adódik. Az excentricitás meghatározásához a két egyenletet vonjuk ki egymásból:
Átrendezés után látjuk, hogy
Behelyettesítés után kapjuk, hogy a példabeli számadatok esetén az üstökös excentricitása e = 0,9545 (négy tizedesjegyre).
3. feladat
Mennyi az (1)-es egyenletben szereplő d állandó értéke?
Megoldás: Nyilván az ellipszispálya bármelyik pontjára felírhatjuk az összefüggést, ugyanazt a d-t kell kapnunk. Ha az égitest a P perihéliumpontban van, akkor távolsága a közelebbi fókuszponttól éppen a napközelség: q=a(1-e), a másik fókuszponttól pedig a+c távolságra van, ahogy az az ábrákból kitűnik. Tehát:
A d állandó tehát éppen az ellipszis nagytengelyének hosszával egyezik meg!
Megjegyzések:
(1) Az I. Kepler-törvényhez megjegyezzük, hogy míg Kepler a bolygók, elsősorban a Mars Tycho által kapott megfigyelési adataival jutott el, Newton a gravitációs törvényből elméleti úton levezette és ugyanazt kapták. Newton eredménye azonban általánosabb, mert elméletileg megfogalmazva az I. Kepler-törvényt az elméleti mechanikában azt mondjuk, hogy “a kölcsönös gravitációs vonzás hatására az egyik pontszerű égitest a másik pontszerű égitest körül kúpszelet alakú pályán mozog: ha az energia minimális, akkor az excentricitás nulla és a pálya kör; ha az energia negatív, akkor az excentricitás nulla és egy közé esik, és a pálya ellipszis alakú; ha az energia nulla (vagyis a gravitációs energia és a mozgási energia egymást semlegesíti), akkor az excentricitás eggyel egyenlő és a pálya parabola alakú; ha pedig az energia pozitív, akkor az excentricitás egynél nagyobb és a pálya hiperbola alakú. (Ha pedig a perdület nulla, akkor a pálya egyenes.)”
A kör, ellipszis, egyenes, parabola és hiperbola mind kúpszeletként kapható meg: egy kúp és egy sík megfelelő szögben történő metszésekor a metszés vonala adja ezeket az alakzatokat. Ezek részleteivel azonban itt nem foglalkozunk, az amatőrcsillagászatban ezek a metszések nagyon ritkán kerülnek elő.
(2) Az I. Kepler-törvény fentiekben írt alakja a valódi anomáliával ezekre az esetekre is érvényes. Mindössze azt kell megjegyezni, hogy hiperbola alakú pályákra a fél nagytengely negatív értéket vesz fel! Mivel a (6)-ik egyenletben az excentricitás egynél nagyobb:
(6) ,
ilyenkor a negatív fél nagytengely a zárójelben lévő negatív kifejezéssel szorzódik és az r távolság pozitív lesz. Némely tankönyvben azonban másként járnak el hiperbola-pálya esetén. A (6)-ik egyenletet csak kör-, ellipszis és parabola pályákra veszik érvényesnek, és hiperbola-pályára
alakot vesznek. Ekkor a hiperbola-pálya fél nagytengelye is pozitív szám lesz. Ez igazából csak konvenció (megállapodás) kérdése, a végeredményben különbség nincs – mindössze azt kell tudnunk, hogy melyik megállapodást követjük. Ebben a cikksorozatban mindig a (6)-ik egyenletet vesszük hiperbolára is, tehát azok pályájának fél nagytengelye negatív szám lesz.
(3) Kepler – mintegy 80 évvel Newton előtt – annyit mondott ki, hogy a bolygók ellipszis alakú pályán keringenek a Nap körül, és a Nap az ellipszis egyik fókuszpontjában áll. Newton mechanikája nyomán tudjuk, hogy Kepler I. törvénye ebben a formában csak akkor igaz, ha a koordinátarendszerünk kezdőpontját (origóját) a Nap (tömeg)középpontjához rögzítjük. Valaki azonban választhat egészen más koordinátarendszert is, pl. egy végtelen távoli megfigyelőhöz rögzítetett, aki olyan messze van, hogy rá a Nap gravitációs vonzóereje már elhanyagolható. (Természetesen Newton szerint hat rá a Nap gravitációja, ha van a megfigyelőnek tömege, de ha nagyon messze van, akkor ez olyan gyenge, hogy elhanyagolható effektust jelent.) Vagy rögzíthetjük egy tömeg nélküli testhez, vagy egy képzeletbeli ponthoz is az origót. Ilyen koordinátarendszerben mindkét égitest a közös tömegközéppont körül fog kúpszelet-alakú pályán mozgást végezni, ahogy a 4. ábra mutatja:
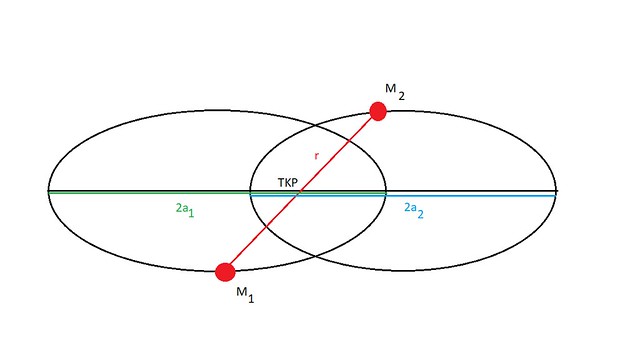
A tömegközéppont az a pont, ami a két testet összekötő r vezérsugarat a tömeggel fordított arányban osztja fel (a fizikában a tömegközéppontot ennél sokkal általánosabban definiálják, de nekünk a Kepler-törvények alkalmazásához ennyi elegendő):
vagy ezzel egyenértékűen: , továbbá igaz, hogy
, ahol a annak a pályának a fél nagytengelye, amit az egyik test ír le a másik körül. Érdemes tudni, hogy a TKP körüli mozgáskör maga a TKP az egyik fókuszpont, de ha az egyik égitestre vonatkoztatjuk a másik mozgását, akkor a másik égitest középpontja a fókuszpont.
Természetesen, a térben ugyanott mozognak a testek. Az alábbi kis animáció mutatja, hogy a testek mozognak a közös tömegközéppont körül, de ha az egyik csillag mozgását a másikra vonatkoztatjuk, akkor az is ellipszispálya lesz:
E fenti videón az látható, hogy két égitest – például két csillag, amelyeket a sárga és a piros korong jelképez – kering a közös tömegközéppont körül. (A közös tömegközéppont mozoghat pl. a Tejútrendszerben és vele együtt a kettőscsillag is, de ez a lényegen már nem változtat.) A két csillag a két, folytonos vonallal rajzolt ellipszisen mozog. E két ellipszis fókuszpontja egyben a közös tömegközéppont. A szaggatott vonallal jelölt ellipszis fókuszpontjában mindig a pirossal jelölt csillag áll! Ez az ellipszis együtt mozog a piros csillaggal. A szaggatott ellipszis nagytengelye a két másik ellipszis nagytengelyének összegével egynelő. Látható, hogy a sárga csillag mindig a piros csillaggal együttmozgó ellipszisen marad, tehát a sárga csillag is ellipszispályán mozog a piros csillag körül, nemcsak a tömegközéppont körül. Szimmetriaokokból hasonló igaz a sárga csillagra is a piros körüli pályáján, de a zsúfoltság elkerülése végett a másik ellipszist nem rajzoltuk be. A pálya fókuszpontja tehát egybeeshet a tömegközépponttal (ha a pályákat a TKP-ra vonatkoztajuk), vagy lehet az egyik csillagban (ha a pályát a másik csillag centrumára vonatkoztatjuk.) Értelemszerűen hasonló igaz a Nap-bolygó, bolygó-hold stb. rendszerekre is. Sőt, ezek a fókuszpontok egyszerre is előfordulnak, hiszen a koordinátarendszereket egyidejűleg is használhatjuk.
Érdekességképpen bemutatjuk, hogy ha körpályán kering egymás körül két pontszerűnek tekinthető égitest, akkor a tömegközéppont körüli pályák körök, de nem meglepő módon az egyik égitest pályája a másik körül szintén kör:
A Naprendszerben a Nap tömege kb. 330 ezerszer nagyobb a Földénél, de még a legnagyobb bolygónál, a Jupiter tömegénél is 1047-szer nagyobb. Ezért a Napnak a közös tömegközéppont körüli pályája a1 fél nagytengelye sokkal kisebb a bolygópályák közös tömegközéppont körüli pályájának a2 fél nagytengelyénél. Annyira, hogy a Nap a1 fél nagytengelye minden bolygóra vonatkoztatva a Nap sugaránál kisebb, tehát a Nap belsejében marad. (Ha az összes bolygó hatását együtt nézzük, akkor nagyon ritkán fordul elő, hogy rövid időre a Nap felszínén kívülre kerül a Naprendszer összes bolygójának és központi csillagának közös tömegközéppontja.) Ezért Kepler nem vehette észre, hogy a közös tömegközéppont és a Nap centruma különbözik a Naprendszerben. Csak sokkal később, a kettőscsillagokál tűnt fel először ez az effektus mérhető mértékben. (Ma már, pl. exobolygók radiális sebességgörbe-méréseiben figyelembe kell venni, hogy a Nap is mozog a TKP körül: a mai radiális sebességgörbe-méréseket már nem a Nap centrumára vonatkoztatjuk, mint régen, hanem a Naprendszer TKP-jára.)
A “Csillagászat elemei” c. cikksorozatban közölt cikkek a szerző engedélye nélkül semmilyen más honlapon, könyvben, cikkben, hírben, stb. nem használhatók fel. Minden jog fenntartva. Lektorálta: Klagyivik Péter.